고정 헤더 영역
상세 컨텐츠
본문
- 이 포스트는 선형대수와 벡터 미적분학-Erwin Kreyszig 개정판을 참고하여 작성되었습니다.
선형연립방정식은 간단히 선형계(linear system)라고도 불리며, 이는 공학, 경제학, 통계학 등 많은 분야의 여러 응용문제에서 나타난다.
선형연립방정식, 계수행렬, 첨가행렬

만일 b 값들이 모두 0이라면 이 선형연립방정식은 homogeneous system이라 한다.
만일 하나라도 0이 아니라면 이 선형연립방정식은 nonhomogeneous system이라 한다.
성분이 연립일차방정식의 해들로 이루어진 벡터를 해벡터(solution vector)라 한다.
선형연립방정식의 행렬표현
행렬곱의 정의로부터, 선형연립방정식을 단 하나의 벡터방정식인 Ax = B로 표현할 수 있다.

이 때 벡터 b를 행렬 A의 오른쪽에 붙인 행렬을 첨가행렬(augmented matrix)이라 한다.
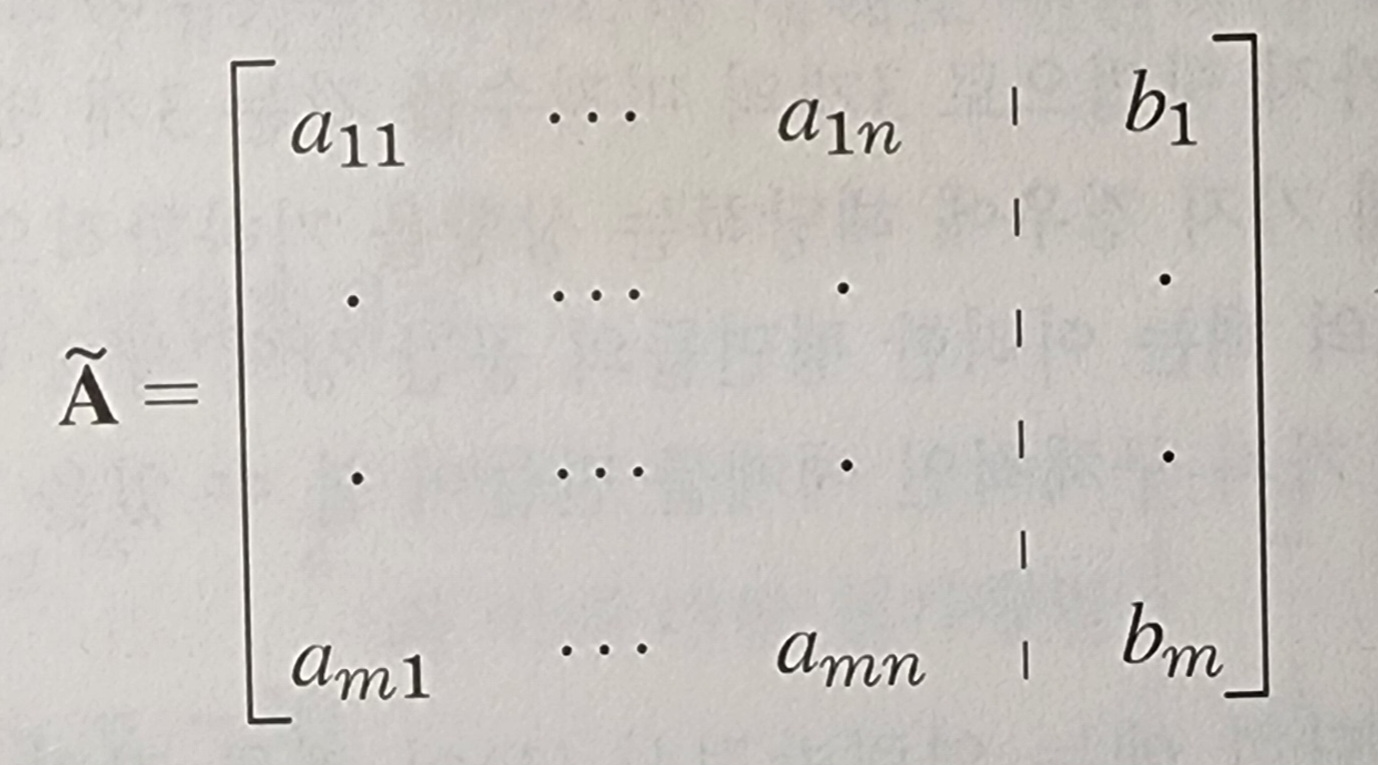
Gauss 소거법과 후치환
후치환(back substitution) 방법이란 아래에 위치한 방정식으로부터 x = b 꼴을 유도한 후 위의 방정식에 대입하는 방법을 말한다.
첨가행렬을 사용해서 후치환 방식을 이용해 해를 구하는 방법을 Gauss 소거법이라 한다.
첨가행렬이 후치환 방식이 가능한 꼴이 되려면 기본 행 연산 과정을 거쳐야 한다. 기본 행 연산(elementary row operation)이란 다음 3가지 연산 방법을 말한다. (항상 행을 중심으로 연산함에 유의)
1. 두 행을 서로 교환
2. 한 행의 상수배를 다른 행에 더하기
3. 한 행에 0이 아닌 상수를 곱하기
기본 행 연산은 아무리 수행해도 해집합은 변하지 않는다는 특징이 있다. 그렇기 때문에 가우스 소거법에서 사용이 가능한 것이다.
'Computer Science > 선형대수학' 카테고리의 다른 글
| 1.6 2차 및 3차 행렬식 (2) | 2023.12.22 |
|---|---|
| 1.5 선형연립방정식의 해: 존재성, 유일성 (2) | 2023.12.22 |
| 1.4 1차 독립. 행렬의 계수(rank). 벡터공간 (0) | 2023.12.22 |
| 1.2 행렬의 곱 (2) | 2023.12.21 |
| 1.1 행렬, 벡터: 합과 스칼라곱 (0) | 2023.12.21 |




