고정 헤더 영역
상세 컨텐츠
본문
- 이 포스트는 선형대수와 벡터 미적분학-Erwin Kreyszig 개정판을 참고하여 작성되었습니다.
행렬식을 여러 가지 방법으로 정의할 수 있지만, 여기서는 선형연립방정식을 다루는 것과 관련된 정의를 소개할 것이다.
n차 행렬직은 n x n 정방행렬에 관한 스칼라 값이며, 아래와 같이 표기한다.
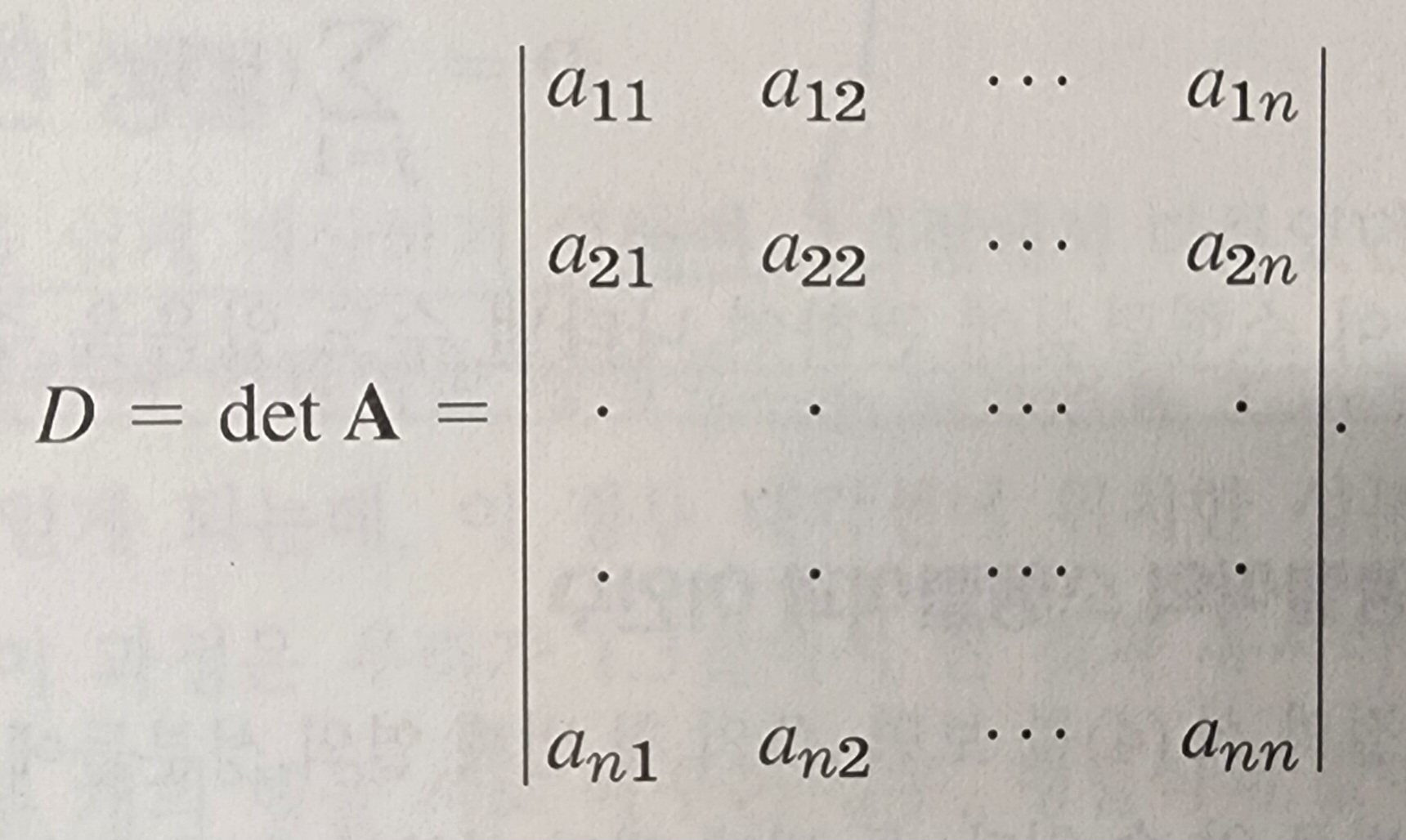
이때 D값은 다음과 같이 정의된다.


Mjk를 소행렬식(minor), Cjk를 여인수(cofactor)라 부른다.
행렬식의 일반적인 성질
행렬식 값을 쉽게 계산하기 위하여, 기본 행 연산을 수행하여 행렬식을 체계적으로 간략화할 수 있다.
기본 행연산(elementary row reduction) 수행 시 n차 행렬식의 변화
1. 두 행을 바꾸면 행렬식의 값에 -1 곱해지게 된다.
2. 한 행의 상수 배를 다른 행에 더하는 것은 행렬식의 값에 변화를 주지 않는다.
3. 한 행에 0이 아닌 c를 곱하면 행렬식의 값이 c배가 된다.
4. 전치(transposition)를 취하여도 행렬식의 값에 변화를 주지 않는다.
행렬식과 계수
m x n 행렬 A가 계수 r(>= 1)을 갖기 위한 필요충분조건은,
1. 행렬 A가 0이 아닌 행렬식을 갖는 r X r 부분행렬을 가진다. (존재)
2. A의 (r+1) x (r+1) 또는 그보다 큰 크기의 모든 정방 부분행렬의 행렬식이 0이 되는 것이다.
Cramer의 법칙
Cramer의 법칙은 계산적인 면에서는 그다지 효율적이지 않으나, 미분방정식 같은 곳에 사용되기 때문에 가치가 있다.
n개의 미지수 x1, ..., xn을 갖는 n개의 선형연립방정식
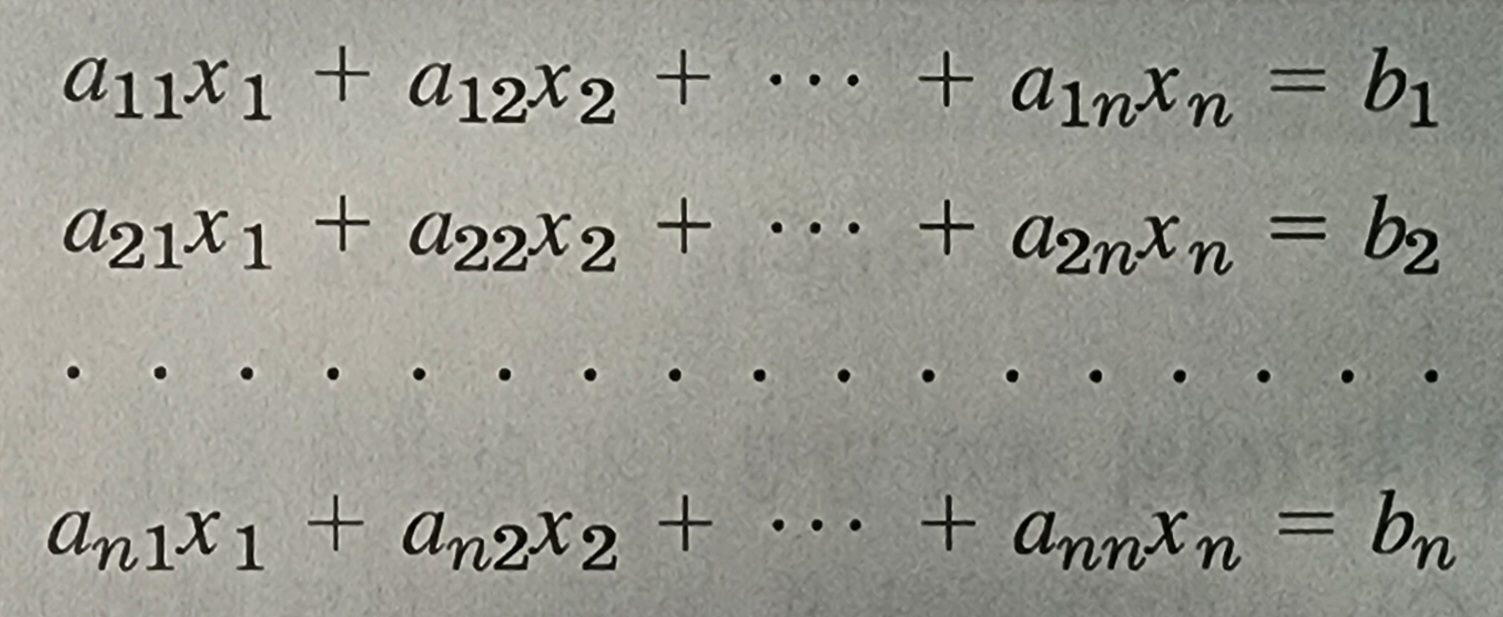
의 계수행렬의 행렬식이 0이 아니면, 그 연립방정식은 오직 하나의 해를 갖고, 그 해는 공식

으로 주어진다. 여기서 Dk는 D의 k번째 열을 상수 열벡터로 대치하여 얻은 행렬식이다.
'Computer Science > 선형대수학' 카테고리의 다른 글
| 1.9 벡터공간, 내적공간, 선형변환 (1) | 2023.12.23 |
|---|---|
| 1.8 역행렬 (1) | 2023.12.23 |
| 1.6 2차 및 3차 행렬식 (2) | 2023.12.22 |
| 1.5 선형연립방정식의 해: 존재성, 유일성 (2) | 2023.12.22 |
| 1.4 1차 독립. 행렬의 계수(rank). 벡터공간 (0) | 2023.12.22 |




