[확률과 통계]4장. 이산확률분포

• 이 포스트는 '공학인증을 위한 확률과 통계 제 4판'을 참고하여 작성되었습니다.

 

 

4.1 이산균등분포

확률변수가 가지는 모든 값에 대하여 대응되는 확률이 전부 같을 때 이 분포를 이상균등분포(discrete uniform distribution)라고 한다.

참고로 확률변수에 대한 확률분포를 결정짓는 상수를 확률분포의 모수(parameter)라고 한다.

 

4.2 초기하분포

초기하분포를 설명하기 위해 다음의 예시를 들어본다.

주머니 속에 M개의 흰색 공이 있고 N-M개의 검은색 공이 있다고 하자. 이 때 n개의 공을 꺼낸다고 했을 때, 이 때 꺼낸 공 중에서 흰색공의 갯수를 확률변수 X라고 하자.

그러면 확률변수 X는 모수 N, M, n인 초기하분포(hypergeometric distribution)를 이룬다고 한다.

표현은 다음과 같다.

초기하분포

초기하분포의 확률질량함수는 다음과 같다.

초기하분포의 확률질량함수

초기하분포의 기댓값은 다음과 같다.

초기하분포의 기댓값

초기하분포의 분산은 다음과 같다.

초기하분포의 분산

 

 

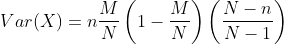
4.3 이항분포

어떤 확률변수는 딱 2가지의 값만 가질 수 있다고 상상해 본다. 그렇다면 하나의 값의 확률이 p라고 한다면 나머지 한 값의 확률은 1-p이다. 이와같은 확률을 가지는 확률변수의 확률분포를 베르누이 분포(Bernoulli distribution)라고 한다.

베르누이 분포의 표시는 다음과 같다.

베르누이 분포

베르누이 분포의 기댓값과 분산은 다음과 같다.

베르누이 분포의 기댓값과 분산

이때 q는 1-p이다.

 

이제 딱 2가지 경우가 성공, 실패라고 생각하고 베르누이 시행을 n번 한다고 하자. 그러면 그 중에서 성공이 발생한 횟수를 확률변수 X라고 한다면 이 확률분포를 모수가 n, p인 이항분포(binomial distribution)라고 한다.

 

이항분포의 확률질량함수는 다음과 같다.

이항분포의 확률질량함수

이항분포의 기댓값과 분산은 다음과 같다.

이항분포의 기댓값과 분산

 

 

4.4 기하분포와 음이항분포

<생략>

 

 

4.5 푸아송분포

한정된 단위 시간이나 공간에서 발생하는 사건의 수에 관련되는 확률모형을 다룰 때 사용되는 확률분포로 푸아송분포가 있다.

(자세한 개념은 매클로린 급수식을 이용해야 하지만 여기서는 생략한다)

어떤 양수 m에 대하여 확률변수 X의 확률질량함수가 다음과 같은 확률분포를 모수가 m인 푸아송분포(Poisson distribution)라 한다.

푸아송분포의 확률질량함수

푸아송분포는 다음과 같이 표현한다.

푸아송분포

푸아송분포의 기댓값과 분산은 다음과 같다.

푸아송분포의 기댓값과 분산

 

 

4.6 다항분포

<생략>