고정 헤더 영역
상세 컨텐츠
본문
- 9월 8일
ㅁㅁ
규제와 라쏘, 릿지회귀
규제
규제(Regularization)란 모델의 과적합을 피하기 위해 가중치에 제한을 거는 방법이다.
-> 과적합된 모델은 가중치 값이 크게 나오는 편이다.
규제는 원래의 Cost Function에 Norm이라는 항을 더하여 그것을 Cost Function으로써 사용한다.
라쏘회귀
라쏘(Lasso)회귀는 L1-Norm 항이 원래의 cost function에 더해진 cost function으로 회귀연산을 하는 회귀를 말한다.
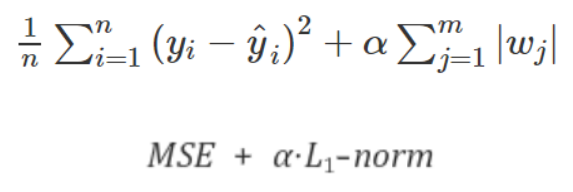
여기서 α는 하이퍼 파라미터로, α가 커질수록 underfitting에 가까워지고, α가 작아질수록 overfitting에 가까워진다.
L1-norm 항에 의해 cost function을 미분하면, 기울기가 음수일 때 wi의 변화량이 +α만큼 더 더해지고, 반대로 기울기가 양수일 때 wi의 변화량이 -α만큼 더 빼진다.
-> 즉 wi의 변화량을 크게 키우는 역할을 한다.
릿지회귀
릿지(Ridge)회귀란 L2-Norm 항이 원래의 cost function에 더해진 cost function으로 회귀연산을 하는 회귀를 말한다.
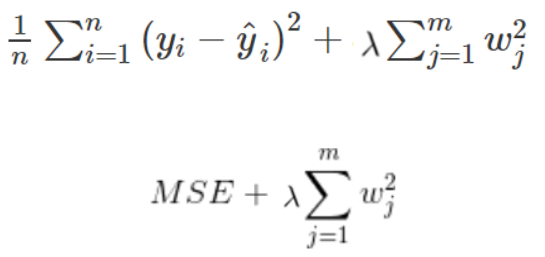
λ는 하이퍼파라미터로, λ가 커질수록 underfitting에 가까워지고, λ가 작아질수록 overfitting에 가까워진다.
L2-norm 항에 의해 cost function을 미분하면, wi의 변화량이 (2λ)x(wi)만큼 추가로 변한다. 즉 가중치 자체를 0값에 가깝게 유도하는 역할을 한다.
로지스틱 회귀
로지스틱 회귀는 분류(classification)에 사용되는 회귀모델로, 특정 라벨에 속하는지 아닌지를 알려주는 알고리즘이다.
회귀알고리즘임에도 불구하고 이진분류에 쓰인다.
선형회귀 방식을 분류에 적용하는 것이기 때문에, 선형회귀 함수로부터 나온 종속변수 값을 Sigmoid라는 함수의 독립변수로 대입하면 된다.
(주의) 로지스틱 회귀를 사용하기 위해선, 먼저 데이터셋을 정규화 해야한다!
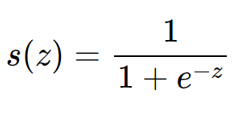
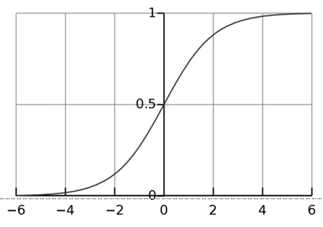
쉽게 말해, 데이터셋이 다음과 같다고 하자.
| x1 | x2 | y |
| 1 | 3 | 5 |
| 3 | 2 | 1 |
| 6 | 9 | 3 |
| 11 | 4 | 4 |
일단 데이터셋을 정규화 시킨다. (아래 StandardScaler를 이용한다)
정규화 시키면 다음과 같다.

이러면 Sigmoid함수의 독립변수 값(입력값)들은 3번째 열이 된다.
(복습) 다음의 용어들은 같은 대상을 가리킨다.
입력벡터 = feature
출력벡터 = target
x절편 = intercept
기울기 = coefficient
로지스틱 회귀 구현
from sklearn.linear_model import LogisticRegression
<logistic_obj> = LogisticRegression()
# StandardScaler를 통해 정규화를 먼저 해 주어야 한다.
<logistic_obj>.fit(<X_train>, <Y_train>)<logistic_obj>.predict(<input_vector>) 함수를 통해 특정 라벨에 속하는지 아닌지를 반환한다.
<logistic_obj>.predict_proba(<input_vector>) 함수를 통해 특정 라벨에 속하는 확률을 반환한다.
특정 라벨에 속하는지 여부를 결정하는 기준은, 확률이 '임계값' 이상이냐 아니냐로 구분한다.
다항 회귀
다항 회귀는 입력벡터의 차수가 2 이상인 회귀 기법이다. 즉 2차, 3차 이상의 방정식으로 표현되는 회귀가 다항 회귀이다.
(주의!) 다항회귀는 선형회귀이다! 왜냐하면 선형/비선형의 판별은 독립변수(입력벡터의 요소들)가 아닌 가중치의 차수로 판별하기 때문이다.
Sklearn 패키지는 다항회귀를 직접적으로 지원하지는 않는다. 따라서 모든 독립변수들의 가능한 항들의 집합으로 입력벡터를 표현해서 사용한다.
예시) x1, x2 두 개의 독립변수가 있는 이차 회귀일때, 입력벡터를 [x1, x2, x1x2, x1^2, x2^2] 으로 구성한다.
일차 회귀였으면 [x1, x2]로만 구성된다.
다항 회귀의 구현
from sklearn.preprocessing import PolynomialFeatures
PolynomialFeatures 함수를 통해 1차 입력벡터를 n차 입력벡터로 변환한다.
예시) [x1, x2] -> [1, x1, x2, x1^2, x1x2, x2^2]
[x1, x2, x3] -> [1, x1, x2, x3, x1^2, x1x2, x1x3, x2^2, x2x3, x3^2]
맨 앞의 1은 상수항에 곱해지는 입력벡터이다. 이것을 원하지 않는다면 include_bias옵션을 F로 하면 된다.
다음 순서대로 n차 입력벡터를 만든다.
<poly_obj> = PolynomialFeatures(degree = <n>[, include_bias = T/F])
<poly_obj>.fit(<np.ndarray>)
<poly_np.array> = <poly.obj>.transform(<np.ndarray>)
include_bias 옵션의 기본값은 True이다.
스케일러
스케일러란 정규화를 해 주는 것을 말한다. 대표적으로 StandardScaler와 MinMaxScaler가 있다.
스케일러를 사용하는 이유
특정 feature에 가중치가 너무 몰리는 것을 방지하기 위해 데이터를 골고루 만들어 주기 위해 사용한다.
스케일러의 종류
StandardScaler는 표준 정규 분포로 변환 해 주는 함수이다.
이상치가 있다면 제거하거나 RobustScaler를 사용한다. (이상치가 mean과 std에 큰 영향을 줌)
-> 시각적으로 보면, 전체 데이터들간의 거리의 비율을 유지한 채, 골고루 퍼지게 하는 역할을 한다.
Normalizer는 각 변수의 값들을 원점으로부터 1만큼 떨어져 있는 구간의 값으로 대응시킨다.
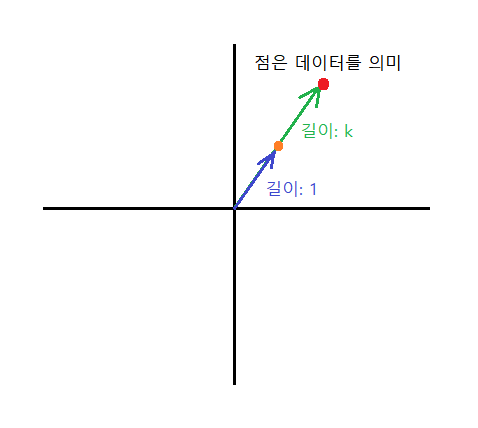
구체적인 feature값들을 뭉개고 feature벡터의 길이를 1로 고정시킨다. 따라서 feature벡터의 원소갯수가 n개라고 할 때, 정보의 갯수가 n개에서 n-1개의 각도로 줄어든다.
MinMaxScaler는 최대/최소 정규화로 변환 해 주는 함수이다.
-> 시각적으로 보면, 전체 데이터들간의 거리의 비율을 유지한 채, 독립변수와 종속변수 모두를 0에서 1 사이로 값을 제한.
RobustScaler는 StandardScaler와 비슷하지만 이상치에 의한 영향이 좀 더 적다.
StandardScaler
<scaled_data> = StandardScaler().fit_transform(<input_data>)
Normalizer
<scaled_data> = Normalizer().fit_transform(<input_data>)
MinMaxScaler
<scaled_data> = MinMaxScaler().fit_transform(<input_data>)
RobustScaler
<scaled_data> = RobustScaler().fit_transform(<input_data>)
(정보) input_data에서 독립변수의 column과 종속변수의 column을 구별하지 않고 통째로 스케일러의 입력으로 넣는 이유는, 독립/종속변수 종류와 상관없이 둘 다 동일하게 스케일링을 하는 것이기 때문이다. 따라서 독립/종속변수 구별을 할 필요가 없다.
만약 feature_data와 target_data가 따로 있다면, fit함수를
'PLAYDATA > PLAYDATA데일리노트' 카테고리의 다른 글
| [PLAYDATA] 데이터 엔지니어링 9월 3주차 9/13 (0) | 2023.09.13 |
|---|---|
| [PLAYDATA] 데이터 엔지니어링 9월 3주차 9/11 (0) | 2023.09.11 |
| [PLAYDATA] 데이터 엔지니어링 9월 2주차 9/7 (0) | 2023.09.07 |
| [PLAYDATA] 데이터 엔지니어링 9월 2주차 9/6 (0) | 2023.09.06 |
| [PLAYDATA] 데이터 엔지니어링 9월 2주차 9/5 (0) | 2023.09.05 |




