고정 헤더 영역
상세 컨텐츠
본문
- 9월 7일
KNN알고리즘과 결정계수, 선형회귀 등에 대해 다룬다
Tip) 지도학습은 분류와 회귀로 나뉜다. KNN은 분류에 해당한다.
KNN 알고리즘
KNN 알고리즘이란 타겟 데이터를 근처 데이터들을 바탕으로 타겟 데이터의 label를 예측하는 알고리즘이다.
-> 여기서 근처라는 것의 기준은, 그래프상 유클리드 거리, 또는 맨하튼 거리가 가장 가까운 것을 뜻한다.
K의 의미
여기서 K의 의미는 근처 데이터를 몇 개까지 수집할 지를 결정하는 값이다.
K개의 이웃 데이터를 수집한 뒤, 가장 많은 라벨을 타겟의 라벨로 예측하게 된다.
특정 두 라벨의 데이터 갯수가 동일해지는 문제를 방지하기 위해, K는 홀수로 정한다.
-> 따라서 K값을 몇으로 하냐에 따라 예측 정확도가 달라진다.
KNN 알고리즘의 구현
(주의!) 모든 데이터들은 그냥 list자료형 보다는 np.reshape(<list>, (M, N))또는 <np.arange함수로 나온 배열>.reshape(M, N)를 통해 np.array자료형으로 변환하여 사용하는걸 권장한다.
1. 하나의 라벨마다 N개의 입력벡터를 준비한다. (파이썬에선 list자료형)
2. 각각의 라벨별로 N개의 입력벡터를 준비한다. (모든 label은 입력벡터 갯수가 n개로 동일해야 한다)
-> 따라서 총 입력벡터 갯수는 Nx(라벨의 종류 갯수) 이다.
3. 모든 라벨에 대해서, 특정 카테고리를 가지는 입력벡터들을 하나로 모두 합쳐 큰 입력벡터로 만든다.
-> 카테고리란, n개의 입력벡터들의 각각의 도메인을 말한다.
4. zip함수를 이용해 데이터 하나를 하나의 좌표로 만든다.
5. label을 element로 하는 타겟벡터를 만든다.
-> <list>*a + <list>*b 등으로 리스트를 간단하게 만들 수 있다. 예를들면 [1]*35 + [0]*14
6. KNN객체를 생성하고 fit함수를 써서 객체에 각 좌표값들을 저장시킨다.
from sklearn.neighbors import KNeighborsClassifier
kn = KNeighborsClassifier()
kn.fit(fish_data, fish_target)
kn.n_neighbors = u를 이용해 K값을 u로 변경 가능
7. KNN객체에 저장된 좌표값들을 이용해서 만들어진 KNN모델을 평가한다.
kn.fit(fish_data, fish_target) -> 1.0이면 전부 맞췄다는 뜻이다.
8. 새로운 좌표 하나를 가지고 <KNN_obj>.predict(<data>)함수를 이용해 모델 사용 가능
KNN 알고리즘의 고려 사항
1. KNN은 좌표상의 거리로 판단하기 때문에, 각 축마다 다루는 값의 범위(그래프를 통해 시각적으로 보면 눈금간격)가 다르다면, 분명 가까운 이웃이라고 생각되는 데이터가 좌표상에서는 굉장히 멀리 떨어져 있는 경우가 발생할 수 있다. 이는 새로운 데이터를 넣었을 때 나의 의도와 다른 label이 출력되는 결과를 낳을 수 있다.
-> 쉽게 예를들자면, 각 입력벡터의 카테고리가 나이와 키(cm)인 경우, 다루는 범위는 나이(0~40), 키(130~200)로 범위가 다르기 때문에 눈금 간격도 다르다.
따라서 일단 각 입력 axis들의 눈금간격을 같게 만드는(범위를 동일하게 설정하는) 작업이 필요하다.
Matplotlib 패키지의 xlim((<min>, <max>)) 그리고 ylim((<min>, <max>)) 그리고 zlim((<min>, <max>))함수들을 사용하여 각 axis의 범위를 지정할 수 있다.
2. 축의 범위를 고정시켰다고 하더라도 데이터들이 실제로 모여있는 범위는 각 축마다 다 다를 수 있다. 예를들어 축의 범위를 나이, 키 모두 0~200으로 고정시켰다면, 나이는 40 밖으로 넘어가지 않기 때문에 나이 축에서 빈 공간이 너무 많이 생긴다. 따라서 궁극적으로 좌표는 각 축의 범위가 같으면서 동시에 각각의 축 기준으로 데이터가 고루 퍼져 있어야 한다.
이를 위해 최소-최대 정규화 방법과 z-score 표준화 방법을 사용한다.
최소-최대 정규화
최소-최대 정규화는 모든 독립변수의 범위를 0~1까지로 나타내도록 변환하는 방식이다.
쉽게말해 모든 축의 범위를 0부터 1까지로 고정시키고, 실제 데이터값의 min이 0, max가 1이 되도록 하여 0~1의 범위안에 데이터가 고루 퍼지도록 만든다.
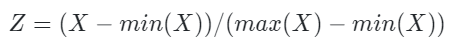
z-score 표준화
z-score 표준화는 모든 axis들을 정규분포화 한다. 따라서 모든 axis가 정규분포를 따르게 되기 때문에 데이터들이 고루 퍼지면서 동일한 정규분포라는 틀에 맞게 된다.
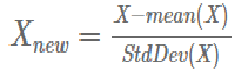
결정 계수
결정계수(R-squared)란 회귀 모델에서 독립변수와 종속변수가 얼마나 잘 결합되어 있는지를 설명하는 지표이다.
단순히 독립변수의 갯수가 증가하는 것 만으로도 증가하는 속성이 있다.
-> 그래서 조정된 결정계수(Adjusted R-squared)라는 개념이 있다.
score함수를 사용해서 모델을 평가할 때 반환되는 값이 바로 결정 계수 값이다. 보통 0.7정도면 양호하다고 간주한다.
결정계수의 공식
결정계수의 식은 다음과 같다.
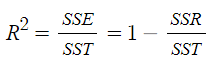
SSE: (추정값-관측값의 평균)^2의 총합이다.
SST: (관측값-관측값의 평균)^2의 총합이다.
SSR: (관측값-추정값)^2(Residual이라고도 함)의 총합이다.
-> 1 - (SSR/SST)인 것을 보면, 관측값과 추정값의 차이가 적을 수록 결정계수는 1에 가까워지며, 많으면 값이 적어진다고 보면 된다.
결정계수 사용
from sklearn.metrics import mean_absolute_error
mean_absolute_error(<target_vector>, <predicted_vector>)
복습) 모델 학습 및 평가 방법
1. 데이터 수집 및 전처리
2. 모델객체를 생성함(예를들어 KNN객체)
3. fit함수 등으로 모델을 학습
4. predict함수를 통해 새로운 값을 예측
5. 결정계수 등을 이용하여 모델을 평가(과적합인가 아닌가 등)
선형 회귀
KNN알고리즘의 설명 및 한계
위의 KNN알고리즘은 데이터들이 특정 label(클래스 라고도 부름. n차원 입력벡터에 대한 결과값이라고 생각)을 가지고 있고 궁극적으로 새로운 데이터가 어떤 label인지를 예측하는 것이다.
KNN알고리즘은 별도의 학습과정(파라미터 값 조정)이 필요하지 않고 단순비교하는 lazy learning(단순암기)알고리즘이다.
그러나 KNN은 새로운 데이터가 기존 기억된 데이터들에게서 너무 멀리 떨어져 있을 경우 정확도가 떨어진다.
그리고 컴퓨터자원을 많이 소모한다.
k값을 알아서 적절하게 조정해야 한다. k가 너무 작으면 overfitting, 너무 크면 underfitting문제가 발생한다.
따라서 이번에는 다른 머신러닝 알고리즘인 선형 회귀에 대해 다룬다.
선형 회귀 개념은 나중에 배울 딥러닝을 이해하는 데에도 사용된다.
선형회귀란?
선형회귀란 가중치를 coefficient로 놓은 뒤, 독립변수들을 1차방정식 형태로 배치하여 1차함수를 이루는 모델이다.
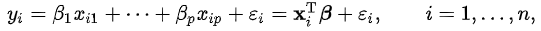

y는 결과값, 종속변수라고 불린다.
x는 입력변수, 독립변수로 불린다.
β는 파라미터, 가중치라고 불린다. 종속변수에 대한 편미분으로 해석할 수도 있다.
ε은 상수, 오차항, 노이즈라고 불린다.
선형 회귀의 원리
선형 회귀의 작동 방향은 SSR을 최소화 하는 것이다. 이 과정을 통해 MSE가 최소 지점이 되는 가중치와 상수를 찾는 것이 선형회귀의 목표이다.
MSE는 Mean Squared Error의 약자로, SSR을 데이터의 갯수로 나눈 값을 말한다.
-> MSE = SUM{(실제값-예측값)^2} / (데이터개수)
가중치, 상수, residual의 관계를 함수로 나타낸 것을 Cost Function이라고 한다.
-> Loss Function이라고도 부른다.
선형회귀의 목표를 달성하기 위해 사용되는 알고리즘을 Optimizer라고 부른다.
경사하강법
경사하강법은 가장 대표적인 optimizer로, cost function의 기울기가 작아지는 방향으로 가중치와 상수를 수정하는 방법이다.
MSE는 데이터 갯수, 실제값, 그리고 추정값(독립변수와 가중치로 이루어져 있다)으로 이루어져 있다. 이때 데이터 갯수는 값이 변하지 않는 상수값이고, "특정" 입력벡터에 대한 실제값을 대입하여 경사하강법을 이용하는 것이기 때문에, 독립변수들과 실제값 부분에 모두 값을 대입하면 남은 미지수는 가중치(w라고 표시한다)와 상수(b라고 표시한다)가 된다. 마지막으로, b는 원래 상수이기 때문에 미분계산을 할 수 없기 때문에 결과적으로 MSE는 w에 대한 함수로 생각할 수 있다.
w는 제곱(^2) 안에 있고, 모든 가중치들(w1, w2, ...)이 1차 형태로 제곱 안에 있기 때문에 MSE는 모든 w에 대하여 2차함수가 된다. 따라서 아래로 볼록한 그래프를 그릴 수 있고 극점이 바로 MSE가 최소가 되는지점, 우리가 찾는 지점이 된다.
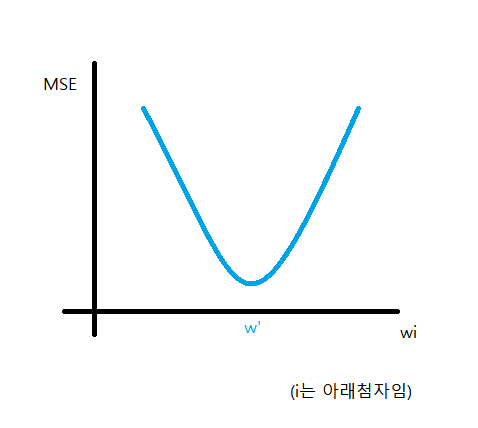
w가 아니라 wi라고 한 이유는, MSE는 가중치가 여러개인(다중선형회귀) 다변수함수이기 때문에 각 가중치마다 최적의 w'을 찾아야 하기 때문이다.
컴퓨터는 극점을 시각적으로 파악하여 바로 찾는것이 불가능하다. 따라서 임의의 값을 wi에 대입하고 기울기가 양수이면 wi를 줄이고, 기울기가 음수라면 wi를 늘리는 것을 반복한다.
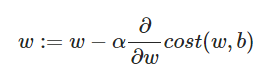
:=의 의미는 right side의 계산을 마치고 left side에 대입하라는 뜻이다. (C언어에서 = 기호 역할을 한다)
cost함수는 MSE를 뜻하며, MSE의 기울기가 (+)이면 기울기를 낮춰야 하기 때문에 기울기 앞에 마이너스를 붙인다.
α는 learning rate라고 하며, 한번에 기울기를 얼마나 변동시킬지를 결정한다. 너무 작으면 학습이 오래 걸리고, 너무 크면 w값이 크게 요동쳐 wi가 극점에 수렴하는게 어려워진다.
-> α와 같은 값을 hyper parameter라고 한다.
(정보) 편미분이란, 변하는 요소가 두 개 이상인 다변수함수에서 하나의 변수에 대해서만 변화양상을 파악하려고 할 때 사용하는 수학 개념이다. 나머지 변수들은 "어떤 값인지는 모르겠지만" "아무튼 고정된 값"으로 간주하고 미분을 하기 때문에, 결과적으로 편미분 된 함수는 모든 나머지 변수들의 조합을 고려한, 대상 변수의 변화량을 의미한다.
Epoch, Batch size 그리고 Iterations
Epoch란 전체 훈련 데이터셋을 학습하는 횟수이다.
Batch size란 경사하강법을 통해서 가중치를 "한 번" 업데이트 할 때 몇개의 데이터를 사용할 지를 결정합니다.
-> GPU의 연산 단위가 됩니다.
Iteration은 한번의 Epoch를 진행하기 위해, 몇 번의 가중치가 갱신되는지를 나타냅니다. (Number of Total Data) / (Batch size)로 표현합니다.
(주의!) Epoch가 2 이상이면, 모든 데이터들에 대해 훈련을 끝내고 처음부터 또 학습을 시작하게 됩니다. Epoch가 너무 높으면 overfitting의 문제가 있습니다.
배치 경사하강법(BGD)
배치 경사하강법이란 전체 훈련 데이터셋을 Batch size(Batch size = Total data)로 갖는 Batch를 사용하여 경사하강법을 수행하는 방법이다.
-> Iteration = 1, 즉 1 Epoch당 가중치 업데이트가 1번만 일어난다.
수렴이 안정적인 장점이 있으나, 규모가 방대해지면 학습 시간이 오래 걸리고 메모리 차지하는 비중이 늘어나 현실적으로 힘들어지는 방법이 된다.
<구현 과정은 생략>
확률적 경사하강법(SGD)
확률적 경사하강법이란 데이터 1개(Batch size = 1)를 무작위로 사용하여 경사하강법을 수행하는 방법이다.
Local Minimum에 갇힐 확률을 줄여주지만 GPU의 병렬 처리 혜택을 잘 활용하지 못한다.
<구현 과정은 생략>
미니 배치 확률적 경사하강법(MSGD)
배치, 확률적 경사하강법의 절충안으로, 지정된 Batch size만큼의 크기를 갖는 Batch를 무작위로 사용하여 경사하강법을 수행하는 방법이다.
<구현 과정은 생략>
Tip) Batch size는 아래 조건을 고려하면 유리하다.
1. Batch size는 2의 제곱 형태가 좋다.
2. (전체 데이터 수) / (Batch size) -> 이것이 가능하면 나누어 떨어지도록 정하고, 그렇지 못한다면 마지막 Batch는 버린다.
최소자승법
<준비중>
선형 회귀의 구현
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
선형회귀 객체 생성
lr.fit(train_input, train_target)
입력벡터의 묶음과 타겟벡터를 넣어서 객체를 학습시킴.
-> 입력벡터가 MxN행렬이라면 타겟벡터는 Mx1행렬이 될 것이다.
lr.predict(<list>)를 통해 입력벡터(1xN행렬)를 넣고 결과값(스칼라)을 확인한다.
lr.coef_로 coefficient를 알 수 있고, lr.intercept_로 상수값을 알 수 있다.
'PLAYDATA > PLAYDATA데일리노트' 카테고리의 다른 글
| [PLAYDATA] 데이터 엔지니어링 9월 3주차 9/11 (0) | 2023.09.11 |
|---|---|
| [PLAYDATA] 데이터 엔지니어링 9월 2주차 9/8 (0) | 2023.09.08 |
| [PLAYDATA] 데이터 엔지니어링 9월 2주차 9/6 (0) | 2023.09.06 |
| [PLAYDATA] 데이터 엔지니어링 9월 2주차 9/5 (0) | 2023.09.05 |
| [PLAYDATA] 데이터 엔지니어링 8월 5주차 8/31 (0) | 2023.08.31 |




